1. 행렬이란?
행렬(Matrix)는 수 또는 문자를 배열의 형태로 나타내는 것을 말한다.

2. 행렬의 크기
행렬의 가로줄은 행(Row), 세로줄은 열(Column)으로 읽는다. 프로그래밍을 할 때에도 많이 쓰이는 영단어이니 확실히 익혀두도록 하자. 만약 햇갈린다면 다음과 같은 방법을 사용해보자.

행렬은 행과 열로 이루어져 있으며, 크기를 나타날때 [행X열] 로 표현한다.
다음과 같은 행렬을 보자.

가로줄(행)이 2개, 세로줄(열)이 3개이니 위 행렬은 2x3 행렬이다.
읽는 방법은 "2행 3열", 또는 "two by three" 행렬이라고 읽어주면 된다.
3. 정방행렬
정방행렬(Square Matrix)는 행과 열의 개수가 같은 행렬을 의미한다.
쉽게 말해 다음과 같은 행렬을 생각하면 된다.

4. 행렬의 연산
1. 덧셈 / 뺄셈

행렬의 덧셈과 뺄샘은 행렬의 크기가 같을 때 연산할 수 있다.
방법은 단순히 각 행렬에서 같은 행과 열 위치의 요소를 더하면 된다.
따라서 위 문제의 답은 다음과 같이 구해진다.

2. 스칼라곱

마치 곱셈연산을 할때 계수를 붙이는 것과 같이, 단순히 각 요소들에 스칼라 값을 곱해주면 스칼라 곱을 구할 수 있다.

3. 곱셈
행렬 A와 B의 곱셈 연산을 하려고 한다면 다음과 같은 조건을 성립해야 한다.
'A의 열 개수와 B의 행 개수가 같을 것'
예를 들어보자. [2x3]과 [3x2]행렬은 행과 열 조건을 충족해 곱셈이 가능하지만, [2x3]과 [2x3] 행렬은 곱셈이 불가능하다.
다르게 말하자면 다음 그림처럼 내측에 있는 수가 같아야지만 곱셈 연산이 가능하다는 것이다.
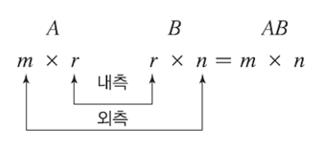
왜냐하면, 행렬의 곱셈은 '열이 행에 대응해 곱해지기' 때문이다.
다음 예제를 보며 이것이 무슨 의미인지 이해해보도록 하자.


예제 (1)을 보도록 하자. 2x3 행렬과 3x1 행렬의 곱이다. 열과 행 조건을 충족시키므로 곱셈이 가능하다.
계산 과정은 다음과 같다.
(1단계)
[1, 2, -1] 행이 [4, 3, 7]에 각각 대응해 곱해진다.
그러므로 [1*4 + 2*3 + (-1)*7]의 값인 3이 결과값의 첫번째 행이 된다.
(2단계)
마찬가지로 [0, -5, 3]행이 [4, 3, 7]에 각각 대응해
[0*4 + (-5)*3 + 3*7] 의 값인 6이 결과값의 두번째 행이 된다.
조금더 복잡한 곱셈을 보도록 하자.
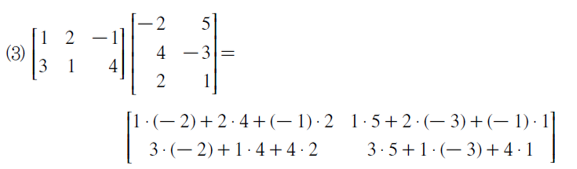
2x3 행렬과 3x2 행렬의 곱셈이다. 열과 행 조건을 충족시키니 곱셈이 가능하다.
계산과정은 다음과 같다.
(1단계)
[1, 2, -1] 행이 [-2, 4, 2] 열에 대응해 곱해진다.
[1*(-2) + 2*4 + (-1*2)] 의 값인 4가 결과값의 [첫번째 행, 첫번째 열]의 요소가 된다.
(2단계)
[1, 2, -1] 행이 [5, -3, 1] 열에 대응해 곱해진다.
[1*5 + 2*(-3) + (-1)*1] 의 값인 -2가 결과값의 [첫번째 행, 두번째 열]의 요소가 된다.
(3단계)
[1, 2, -1] 행이 [5, -3, 1] 열에 대응해 곱해진다.
(계산과정 생략) 의 값인 6이 결과값의 [두번째 행, 첫번째 열]의 요소가 된다.
(4단계)
[1, 2, -1] 행이 [5, -3, 1] 열에 대응해 곱해진다.
.(계산과정 생략) 의 값인 16이 결과값의 [두번째 행, 두번째 열]의 요소가 된다.
따라서 위 곱셈의 계산 결과는 다음과 같다.

.
.
'수학 > 이산수학' 카테고리의 다른 글
| [이산수학] 가우스 (조던) 소거법, (기약) 행 사다리꼴 (3) | 2020.10.16 |
|---|---|
| [이산수학] 역행렬 구하기 - 수반행렬을 이용한 방법 (0) | 2020.10.03 |
| [이산수학] 행렬식의 개념 - 그래서 3*3행렬식은? (0) | 2020.09.25 |
| [이산수학] 행렬식의 개념 - 2*2 행렬 중심으로 (0) | 2020.09.25 |
| [이산수학] 행렬 기본 - 행렬법칙과 특수행렬들 (0) | 2020.09.11 |